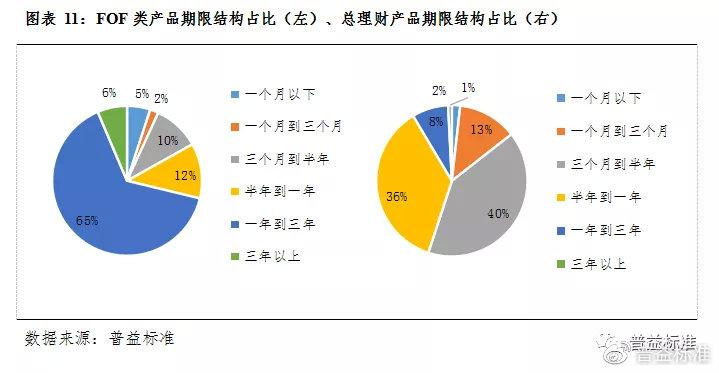
波函数匹配的新方法有助于解决量子多体问题

波函数匹配是指在量子力学中对不同体系的波函数进行比较和匹配的过程。对于量子多体问题，即涉及多个粒子的相互作用的问题，传统方法往往难以处理复杂的相互作用关系和大量自由度的系统。然而，近年来出现的一些新方法在解决量子多体问题时表现出了巨大的潜力。

密度泛函理论(DFT)与波函数匹配

密度泛函理论是一种处理多体量子系统的有效工具，它通过电子的密度来描述系统的基态性质，并能够在一定程度上准确描述原子和分子的结构、振动、电子云等性质。在密度泛函理论中，波函数匹配被用来比较不同电子密度下的基态波函数，从而得到系统的能量和其他物理性质。近年来，一些改进的密度泛函方法，如非局域密度泛函理论和经验密度泛函理论，通过引入更精细的电子相关性来提高对多体问题的描述能力。

量子蒙特卡洛方法(QMC)与波函数匹配

量子蒙特卡洛方法是一种数值计算技术，通过蒙特卡洛随机抽样来解决量子系统的基态性质，并且在处理多体问题时展现出了较高的精确度。最近的一些研究表明，结合波函数匹配技术和量子蒙特卡洛方法，可以更准确地描述多体系统的基态波函数，从而得到更可靠的能量和相关性质。

张量网络方法与波函数匹配

张量网络方法是一种处理多体量子系统的新型数值技术，它通过构建张量网络来描述系统的波函数，并能够高效地处理系统中的相互作用和自由度。近年来，一些新的张量网络方法，如基于机器学习的自动编码器和变分量子饱和度矩阵方法，利用波函数匹配技术来优化张量网络的结构和参数，从而更好地描述复杂的多体系统。

结语

波函数匹配的新方法在解决量子多体问题时具有重要的意义。这些方法不仅在处理多体系统的基态波函数和能量计算上具有优势，而且为研究多体系统的动力学性质和相关性质提供了新的途径。在未来的研究中，可以进一步探索和发展这些方法，以解决更复杂和实际的量子多体问题。